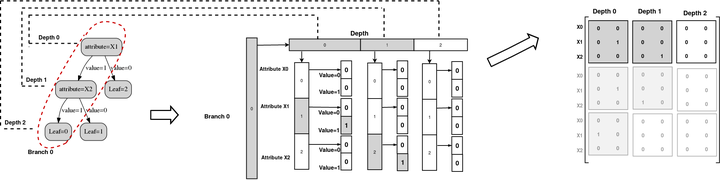
 Our tree representation to allow the formalisation of a broad class of constraints .
Our tree representation to allow the formalisation of a broad class of constraints .
Abstract
When applied to critical domains, machine learning models usually need to comply with prior knowledge and domain-specific requirements. For example, one may require that a learned decision tree model should be of limited size and fair, so as to be easily interpretable, trusted and adopted. However, most state-of-the-art models, even on decision trees, only aim to maximising expected accuracy. In this paper, we propose a framework in which a diverse family of prior and domain knowledge can be formalised and imposed as constraints on decision trees. This framework is built upon a newly introduced tree representation that leads to two generic linear programming formulations of the optimal decision tree problem. The first one targets binary features, while the second one handles continuous features without the need for discretisation. We theoretically show how a diverse family of constraints can be formalised in our framework. We validate the framework with constraints on several applications and perform extensive experiments, demonstrating empirical evidence of comparable performance w.r.t. state-of-the-art tree learners.
